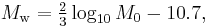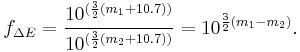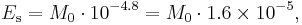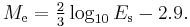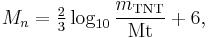Moment magnitude scale

The moment magnitude scale (abbreviated as MMS; denoted as Mw) is used by seismologists to measure the size of earthquakes in terms of the energy released.[1] The magnitude is based on the moment of the earthquake, which is equal to the rigidity of the Earth multiplied by the average amount of slip on the fault and the size of the area that slipped.[2] The scale was developed in the 1970s to succeed the 1930s-era Richter magnitude scale (ML). Even though the formulae are different, the new scale retains the familiar continuum of magnitude values defined by the older one. The MMS is now the scale used to estimate magnitudes for all modern large earthquakes by the United States Geological Survey.[3]

Contents

Definition

The symbol for the moment magnitude scale is 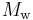M_\mathrm{w}, with the subscript 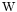\mathrm{w} meaning mechanical work accomplished. The moment magnitude 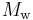M_\mathrm{w} is a dimensionless number defined by

M_\mathrm{w} = \textstyle{\frac{2}{3}}\log_{10}M_0 - 10.7,

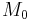where M_0 is the magnitude of the seismic moment in dyne centimeters (10−7 Nm).[1] The constant values in the equation are chosen to achieve consistency with the magnitude values produced by earlier scales, most importantly the Local Moment (or "Richter") scale.

As with the Richter scale, an increase of 1 step on this logarithmic scale corresponds to a 101.5 ≈ 30 times increase in the amount of energy released, and an increase of 2 steps corresponds to a 103 = 1000 times increase in energy.

Comparative energy released by two earthquakes

A closely related formula, obtained by solving the previous equation for 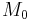M_0, allows one to assess the proportional difference 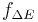f_{\Delta E} in energy release between earthquakes of two different moment magnitudes, say 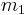m_1 and m_2:

f_{\Delta E} = \frac{10^{(\frac{3}{2}(m_1 + 10.7))}}{10^{(\frac{3}{2}(m_2 + 10.7))}} = 10^{\frac{3}{2}(m_1 - m_2)}.

Radiated seismic energy

Potential energy is stored in the crust in the form of built-up stress. During an earthquake, this stored energy is transformed and results in

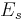The seismic moment 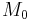M_0 is a measure of the total amount of energy that is transformed during an earthquake. Only a small fraction of the seismic moment 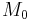M_0 is converted into radiated seismic energy 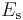E_\mathrm{s}, which is what seismographs register. Using the estimate

E_\mathrm{s} = M_0\cdot10^{-4.8}=M_0\cdot1.6\times10^{-5},

Choy and Boatwright defined in 1995 the energy magnitude [4]

M_\mathrm{e} = \textstyle{\frac{2}{3}}\log_{10}E_\mathrm{s}-2.9.

Nuclear explosions

The energy released by nuclear weapons is traditionally expressed in terms of the energy stored in a kiloton or megaton of the conventional explosive trinitrotoluene (TNT).

A rule of thumb equivalence from seismology used in the study of nuclear proliferation asserts that a one kiloton nuclear explosion creates a seismic signal with a magnitude of approximately 4.0. [5] This in turn leads to the equation [6]

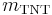M_n = \textstyle\frac{2}{3}\displaystyle\log_{10} \frac{m_{\mathrm{TNT}}}{\mbox{Mt}} + 6,

where m_{\mathrm{TNT}} is the mass of the explosive TNT that is quoted for comparison (relative to megatons Mt).

Such comparison figures are not very meaningful. As with earthquakes, during an underground explosion of a nuclear weapon, only a small fraction of the total amount of energy transformed ends up being radiated as seismic waves. Therefore, a seismic efficiency has to be chosen for a bomb that is quoted as a comparison. Using the conventional specific energy of TNT (4.184 MJ/kg), the above formula implies the assumption that about 0.5% of the bomb's energy is converted into radiated seismic energy 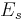E_s.[7] For real underground nuclear tests, the actual seismic efficiency achieved varies significantly and depends on the site and design parameters of the test.

Comparison with Richter scale

Main article: Richter magnitude scale

In 1935, Charles Richter and Beno Gutenberg developed the local magnitude (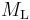M_\mathrm{L}) scale (popularly known as the Richter scale) with the goal of quantifying medium-sized earthquakes (between magnitude 3.0 and 7.0) in Southern California. This scale was based on the ground motion measured by a particular type of seismometer at a distance of 100 kilometres (62 mi) from the earthquake. Because of this, there is an upper limit on the highest measurable magnitude; all large earthquakes will have a local magnitude of around 7. The local magnitude's estimate of earthquake size is also unreliable for measurements taken at a distance of more than about 350 miles (600 km) from the earthquake's epicenter.[3]

The moment magnitude (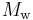M_\mathrm{w}) scale was introduced in 1979 by Caltech seismologists Thomas C. Hanks and Hiroo Kanamori to address these shortcomings while maintaining consistency. Thus, for medium-sized earthquakes, the moment magnitude values should be similar to Richter values. That is, a magnitude 5.0 earthquake will be about a 5.0 on both scales. This scale was based on the physical properties of the earthquake, specifically the seismic moment (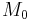M_0). Unlike other scales, the moment magnitude scale does not saturate at the upper end; there is no upper limit to the possible measurable magnitudes. However, this has the side-effect that the scales diverge for smaller earthquakes.[1]

Moment magnitude is now the most common measure for medium to large earthquake magnitudes,[8] but breaks down for smaller quakes. For example, the United States Geological Survey does not use this scale for earthquakes with a magnitude of less than 3.5, which is the great majority of quakes. For these smaller quakes, other magnitude scales are used. All magnitudes are calibrated to the 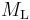M_\mathrm{L} scale of Richter and Gutenberg.

Magnitude scales differ from earthquake intensity, which is the perceptible moving, shaking, and local damages experienced during a quake. The shaking intensity at a given spot depends on many factors, such as soil types, soil sublayers, depth, type of displacement, and range from the epicenter (not counting the complications of building engineering and architectural factors). Rather, they are used to estimate only the total energy released by the quake.

The following table compares magnitudes towards the upper end of the Richter Scale for major Californian earthquakes.[1]

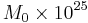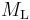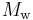Date M_0\times10^{25} M_\mathrm{L} M_\mathrm{w}
1933-03-11 2 6.3 6.2
1940-05-19 30 6.4 7.0
1941-07-01 0.9 5.9 6.0
1942-10-21 9 6.5 6.6
1946-03-15 1 6.3 6.0
1947-04-10 7 6.2 6.5
1948-12-04 1 6.5 6.0
1952-07-21 200 7.2 7.5
1954-03-19 4 6.2 6.4

See also

Notes

  1. ↑ 1.0 1.1 1.2 1.3 Hanks, Thomas C.; Kanamori, Hiroo (05/1979). "Moment magnitude scale". Journal of Geophysical Research 84 (B5): 2348–2350. doi:10.1029/JB084iB05p02348. http://adsabs.harvard.edu/abs/1979JGR....84.2348H. Retrieved 2007-10-06. 
  2. ↑ "Glossary of Terms on Earthquake Maps". USGS. http://earthquake.usgs.gov/eqcenter/glossary.php#magnitude. Retrieved 2009-03-21. 
  3. ↑ 3.0 3.1 USGS Earthquake Magnitude Policy
  4. ↑ Choy, George L.; Boatwright, John L. (1995), "Global patterns of radiated seismic energy and apparent stress", Journal of Geophysical Research 100 (B9): 18205–18228, http://www.agu.org/pubs/crossref/1995/95JB01969.shtml 
  5. ↑ "Nuclear Testing and Nonproliferation", "Chapter 5: Assessing Monitoring Requirements"
  6. ↑ "What is Richter Magnitude?"
  7. ↑ Q: How much energy is released in an earthquake?
  8. ↑ Boyle, Alan (May 12, 2008). "Quakes by the numbers". MSNBC. http://cosmiclog.msnbc.msn.com/archive/2008/05/12/1012798.aspx. Retrieved 2008-05-12. "That original scale has been tweaked through the decades, and nowadays calling it the "Richter scale" is an anachronism. The most common measure is known simply as the moment magnitude scale." 

References

  • Choy GL, Boatwright JL (1995). "Global patterns of radiated seismic energy and apparent stress". Journal of Geophysical Research 100 (B9): 18205–28. doi:10.1029/95JB01969. 
  • Utsu,T., 2002. Relationships between magnitude scales, in: Lee, W.H.K, Kanamori, H., Jennings, P.C., and Kisslinger, C., editors, International Handbook of Earthquake and Engineering Seismology: Academic Press, a division of Elsevier, two volumes, International Geophysics, vol. 81-A, pages 733-746. 

External links

Seismic scales
Modern scales
Intensity scales
European Macroseismic Scale (EMS) · INQUA · Liedu · Medvedev-Sponheuer-Karnik (MSK) · Modified Mercalli (MM) · Shindo
Magnitude scales
Body wave magnitude · Local magnitude (Richter scale) · Moment magnitude · Surface wave magnitude
Historical scales